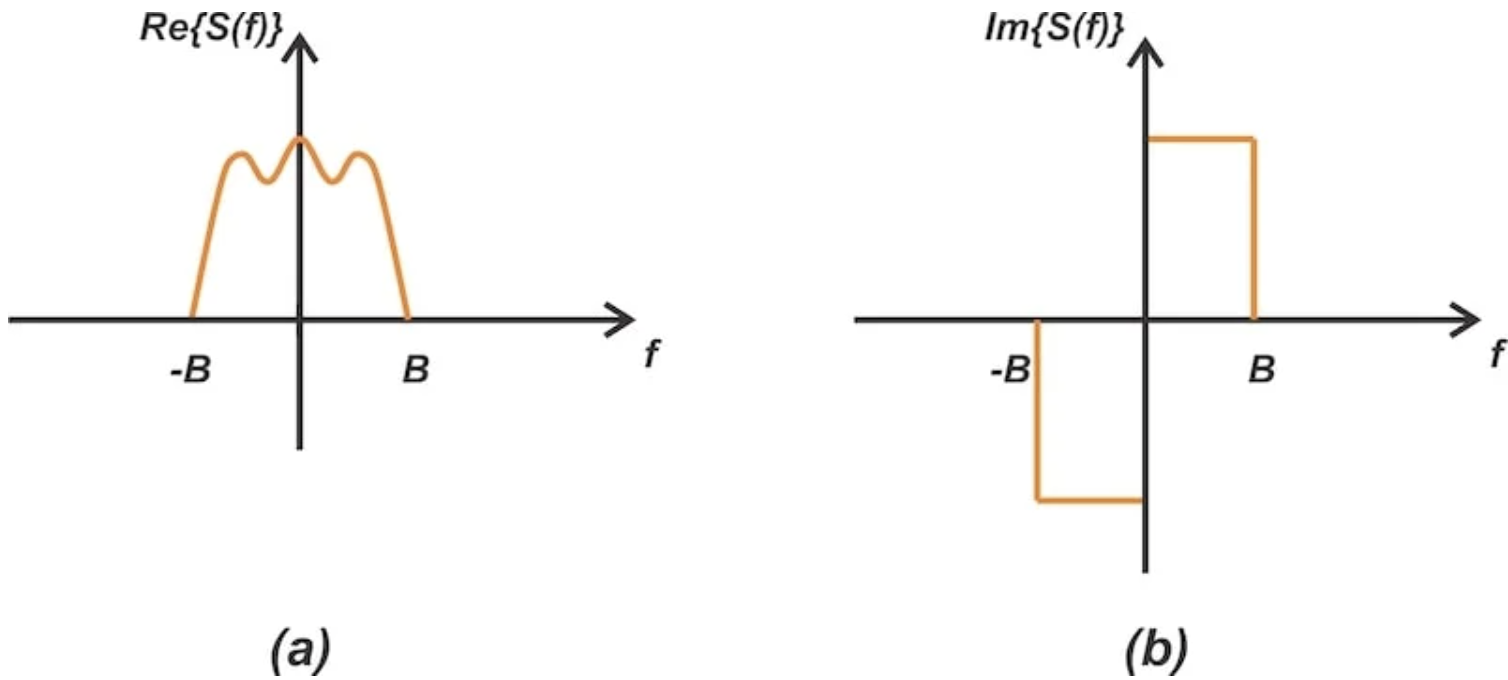使用相音量，我们探讨了如何真正有价值的带通信号表示为RF通信系统中使用的模型中的复杂基带信号。提到本文的地址：带通信号和系统对通信系统很重要。有趣的是，真正有价值的带通信带来的所有信息都包含在相应的复杂基带信号中。该基带的复杂表示对于理解无线电通信系统非常有用。在本文中，我们将了解带通信号的复杂基带表示。作为讨论的一部分，我们还将探讨交流电路中Phamor分析的概念。但是，在我们深入研究之前，让我们回顾一下低通信号和信号ng bandpass的定义，以确保我们拥有基础知识。当信号的频率含量或频谱以零频率为中心时，低通过和带信号的信号称为低通信号。换句话说s，低通信号具有明显的带宽B，并且对于if的频率。图1显示了其频谱的含量。图1显示了低通信号的真实和虚构组件。图1。带宽B带带宽B的真正有价值的低通信号的实际部分（a）和假想部分（b）。请注意，如果s（t）是一个真正有价值的功能，则更改s（f）的傅立叶将显示共轭的对称性。这意味着S（f）的真实部分是一个均匀的函数，并且猜测是一个唯一的函数。另一方面，BandPass的信号频谱频率是FC频率的Nakasenter，该频率大于信号带宽B。图2显示了带通信号的真实和想象中的部分。图2。具有FC中心频率和B带宽的真实带通信号值的频谱分为实际零件（a）和虚部（b）。与图1中的基带光谱相似，图2还显示了共轭对称性，因为信号是真的。真实信号的带宽定义为信号中频率含量的所有正组件的长度。如果最高和最低的正信号频率分别为fmax和fmin，则信号的带宽为：b = fmax-fmin，根据上述定义，单频率电影波（FC FC和振幅A）的带宽为零。但是，s（t）= acos（ωct+θ），但是，如果随着时间的推移变化速度慢，那么我们将获得非零带宽的振幅（am）调制。交流电路中的phamor表明相量是一个复杂的数字，代表正弦波形的振幅和相位角度。在交流电路分析中，使用方法用于研究频率相关效应。例如，考虑一个单一的频率电影波，如等式2所示。此信号是复杂操作的真实部分：s（t）= re {[aejθ]ejΩct}，其中操作员re {走气{走气}代表括号中体积的真实部分。我们可以代表wi在具有振幅A和θ的初始阶段的复杂平面中，这是一个括号。如图3所示，该信号以ωc=2πfc的角速度围绕源旋转。单频部电影波的相表达图3。单频NA电影波的相表达。该矢量在真实轴上的投影（即，实际部分）产生了公式2中显示的原始信号。角度ωct的角度代表以每秒FC超速速度的稳定逆时针旋转。为了获得简化的信号表示形式，我们将忽略此项目。去除周期后，获得了固定向量，该载体与等式3中的括号中的项一致。该独立项是与我们的信号相关的量词。以下公式提供了以下操作：s〜 =aejθ以了解Phamor表示的含义，可以考虑通过电影输入激发的线性时间不变（LTI）系统。如图4所示，这种激发形成了SI所有电路节点处的鼻子信号。尽管所有这些信号都具有频率，但它们的幅度和相位可能会有所不同。 LTI电路产生的正弦信号可以在相曲仪中表达，具有不同的振幅和初始相，但以相同的角速度旋转。图4。通过LTI电路产生的正弦信号可以在相曲线中表达，具有不同的幅度和初始相，但以相同的角速度旋转。因为所有这些向量都以相同的角速旋转，所以它们之间的相位差异不会随时间变化。这些向量的幅度比也独立于时间。因此，我们可以让扭曲的向量进入某个时刻。从电压和电流值中删除时间依赖项，从而使我们可以将它们表示为复杂的值，独立的时间数。 Lubos简化了电路检查。当我们计算一定电压或电流值的向量时，我们可以重新创建一部分循环以确定NE该量的域的实际表达。简而言之，拟光者消除了预期时间的复杂性，从而更容易描述电压和电流音量。用外行的话来说，您可以想象相思是单频电影浪潮的低通或直流。将相当于调制的带通信号等效的低通信号降低到今天，我们假设正弦波的幅度和相位是固定的。但是，相同的测试也可以应用于FC频率的电影波，其幅度和相位随时间变化。假设以FC为中心的调制波被指定为：srf（t）= a（t）cos（ωct+θ（t）），其中a（t）和θ（t）是变化时间的直接振幅和信号阶段。上面的公式可以重新编写为：srf（t）= re {[[a（t）ejθ（t）]ejΩct}公式7分隔括号中的术语：sl（t）= a（t）ejθ（t）ejθ（t）此术语是带通道信号的复杂表示。以上fOrmula也可以以笛卡尔形式表达：SL（t）= Si（t）+JSQ（T），其中（T）和SQ（T）是具有等效基带信号SL（T）的相位内和正交成分的物质。这些组件由以下公式提供：si（t）= a（t）cos（θ）和sq（t）= a（t）sin（θ），因为带路信号的相位内和正交组件很慢，我们知道它们都是低通信号。 Replace SL (T) cartesian form with equation 6, and we can use the substance in-phase and orthogonal components upg represents the original RF signal: SRF (T) = (T) COS (ωCT) -Sq (T) Sin (ωCT) The above formula shows that the bandpass signal can be represented by two low-pass signals, its namelys-phase components and orthogonal components.低通信号等效：可视表低通路低通表示可以将其视为与源头（SI-SQ）复合面的起点变化的时代。这在图5中描述了图5。使用基带信号SL（t）用作与平面（SI-SQ）平面变化的时间。由于物质内和正交分量（t）和SQ（t）分别是时间函数，因此相端的末端移至（Si-SQ）平面。从公式6可以看出，等效基带信号sl（t）乘以复杂的指数ejΩct生成thebandpass信号SRF（t）。因此，向量sl（t）和（Si -sq）平面以ωc=2πfc的角速度旋转。图6。在包含旋转部分的复杂平面中的Phamor多样性。原始的带通信号SRF（t）是该伪造时间在代表真轴的固定线中的时间去除的投影。固定的带通信号方程式10立即告诉我们如何通过相位和正交组件重建带通信号。图7显示了从低通到频段传递的转换电路。阻止从低通相和正交开发带通信号的图表信号。接下来，我们需要确定带通信号的等效基带信号。我们首先将SRF（t）乘以2coS（ωct）：srf（t）×2cos（ωct）= a（t）cos（ωct+θ（t））×2cos（ωct）= a（t）= a（t）[cos（2Ωct+θ（t））low pass（2Ωct+θ（t）low pass [srf（t）cos（t） the same, srf (t) by −2sin (ωct) produces: srf (t) Cos (ωCT+θ (T)) × (−2sin (ωCT)) = -a (T) [fault (2ωct+θ (t))-sin (θ (t))] application of a suitable low-pass filter can remove the signal substances twice the carrier frequency, and get: lowpass [SRF (T) A （t）SIN（θ（t））= SQ（T）图8显示了如何使用一对乘数和一对低通滤波器实现公式12和14。图8。从带通信号中阻止低通同时开发图和正交信号。总结有关带通信号真实值的所有信息都包含在相应的复杂基带信号中。在本文中，我们学会了如何扣除等于带通信号的信号，反之亦然。它值得注意的是，该讨论的扩展使我们能够使用复杂的低通滤波器代表带通滤波器。这是为带通信号和过滤器建立低通模型的重要意义。例如，现代通信收发器将这些模型应用于自动处理复杂的基带信号，从而减少了对带通信号的模拟处理的需求。图7和8中显示的电路对于理解线性调制方案（无论是模拟还是数字）都很重要。在下一篇文章中，我们将看到织布工调制器如何使用这些电路来产生单个边界AM信号。